Puntuaciones con EvalCOMIX-FLOASS
Las puntuaciones que se otorgan con los instrumentos EvalCOMIX se presentan en una escala 0-100, de tal forma que el primer valor asignado será 0 y el último 100, de acuerdo a la siguiente secuencia aritmética:
P = {0, d, d+d, d+d+d,..., 100}
Como se observa, cada término se diferencia del siguiente por una distancia constante d.
¿Cómo se calcula d?
El cálculo de d se realiza de la siguiente manera: d = 100 / (n - 1), siendo n el número de grados de la escala que se utilice.
Por ejemplo, para la escala E = {1, 2, 3, 4, 5}, n = 5 y, por tanto, d = 100 / (5 - 1), es decir, d = 25. Por consiguiente, P = {0, 25, 50, 75, 100}
|
Escala |
1 |
2 |
3 |
4 |
5 |
|
Puntuación |
0 |
25 |
50 |
75 |
100 |
Para la escala E = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10}, n = 11 y, por tanto, d = 100 / (11 - 1), es decir, d = 10.
De esta forma, cuando se puntúa quedaría el siguiente esquema de calificación:
|
Escala |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
Puntuación |
0 |
10 |
20 |
30 |
40 |
50 |
60 |
70 |
80 |
90 |
100 |
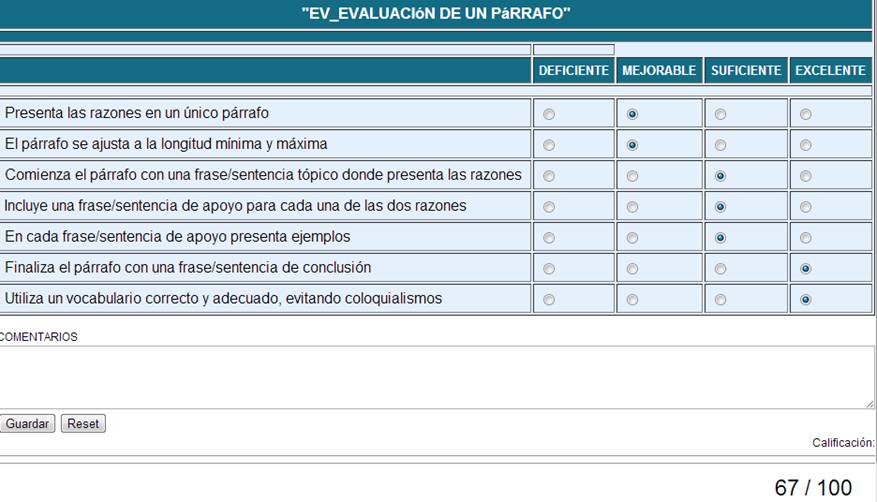
Veamos una aplicación práctica con instrumentos de EvalCOMIX. En la Figura 1 se presenta una escala de valoración con 4 grados (deficiente, mejorable, suficiente y excelente). Por lo tanto, d=100/(4-1)= 33,3. Así pues, las puntuaciones serán:
|
Escala |
Deficiente |
Mejorable |
Suficiente |
Excelente |
|
Puntuación |
0 |
33,3 |
66,6 |
99,9 |
En el caso de la figura 1, las puntuaciones han sido:
33,3 + 33,3 + 66,6 + 66,6 + 66,6 + 99,9 + 99,9 = 466,2/ 7 = 66,6 (Se redondea a 67)
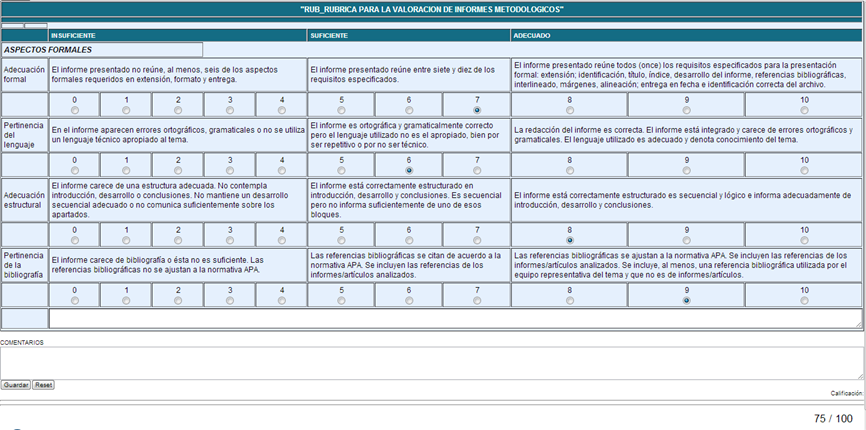
En la Figura 2 se presenta una rúbrica que presenta una escala E = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10}, n = 11 y, por tanto, d = 100 / (11 - 1), es decir, d = 10.
De esta forma, cuando se puntúa quedaría el siguiente esquema de calificación:
|
Escala |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
Puntuación |
0 |
10 |
20 |
30 |
40 |
50 |
60 |
70 |
80 |
90 |
100 |
Las puntuaciones han sido: 70 + 60 + 80 + 90 = 300 / 4 = 75.